記憶バックアップ作戦
・2次方程式の解(その8)
[x=-(√(17)+3)/2,x=(√(17)-3)/2]
CF) T:数学教師
S:生徒
T:「君がもしも電気のない無人島に流されたとしたら、この方法は通用しない。」
S:「はぁ。」
T:「私は、紙と鉛筆だけで計算できる方法を教えているわけだ。」
S:「でも、無人島には紙も鉛筆もないでしょ。」
T:「砂と君の指があれば十分だよ。」
S:「そんな生活をしていて、2次方程式を解かねばならない事態に遭遇するとは思えませんが。」
T:「そうくると思っていたよ。」
S:「・・・。」
T:「そのときには、先生のことを思い出して懐かしんでくれると嬉しいんだが。」
・2次方程式の解(その9)
理想形を追求する方法を説明しましょう。
まず、
(x+y)^2=x^2+2・x・y+y^2
を思い出します。
右辺の係数比は、1:2:1できれいな数値です。
a・x^2+b・x+c=0
の左辺の係数比はa:b:cですが、
これを1:2:1にしてみせようではないか(なーんちゃって)。
x=y/zとおいて、
a・(y/z)^2+b・(y/z)+c=0
a・y^2+b・z・y+c・z^2=0
係数比a:b・z=1:2とするには、z=(2a)/bとします。
a・y^2+2・a・y+c・z^2=0
a・(y^2+2・y+1)=a-c・z^2
a・(y+1)^2 =a-c・((2・a)/b)^2=0
(y+1)^2 =1-(4a・c)/b^2
左辺を理想形に変形してキレイにすると、
右辺にはお世辞にもキレイとはいえないものが出てきます。
y+1=±(√(b^2-4a・c))/|b|
y=-1±(√(b^2-4a・c))/|b|
∴ x=y/z=(b/(2a))(-1±(√(b^2-4a・c))/|b|)
例1)
2x^2+4x+1=0
これは、2:4=1:2が明らかですので、
両辺に1を加えます。
2x^2+4x+2=1
2(x+1)^2=1
(x+1)^2=1/2
x+1=±1/√2
∴ x=-1±√2/2
例2)
5x^2+4x+2=0
左辺の1次項の係数と定数の比に4:2=2:1がみえます。
x=y/zとおいて
5(y/z)^2+4(y/z)+2=0
5y^2+4(y・z)+2z^2=0
2z^2+4(y・z)+5y^2=0
y=1とおけば、2:4y=1:2になります。
2(z^2+2z+1)=2-5y^2=-3
2(z+1)^2=-3
z+1=±(√(3/2))i :iは虚数単位
z=-1±(√(3/2))i
∴x=y/z=1/z
これで終わりにできないのが、この方法の欠点ですが、致命的ではありません。
ここで思い出してほしいのは、zの複素共役z*
1/z=z*/(zz*)
分母zz*
はzの絶対値の2乗で、実数部(-1)の2乗と虚数部(√(3/2))の2乗の和です。
=1+3/2=5/2
よって
x=(2/5)(-1±(√(3/2))i)
=(-2±(√6)i)/5
以上、1:2:1を勝手に理想的な比とデッチアゲテ計算しましたが、
諸君の好きな比でやってみてください(といっても、そんな暇人はいねーだろー)。
121=11^2
144=12^2
169=13^2 etc.
ピタゴラスの定理
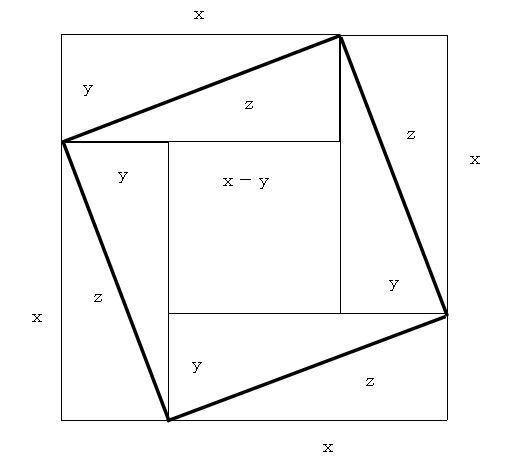
この図と同様のものが、今から二千年以上も前に、y:x:z=3:4:5の比率で描描かれていたことを知ったときには感心しました。ピタゴラスの定理は、彼が証明したときよりもさらに二千年以上前に発見されていたらしいとのことです。
ユークリッド先生が行った証明は私にはとても記憶できるような代物ではありません。以下の証明は、上図を記憶できるかどうかにかかっています。
大きい方の正方形から、
□(x+y)=4・⊿(x,y)+□(z)
小さい方の正方形から、
□(z)=4・⊿(x,y)+□(x-y)
が分かります。
□(A)=A・A :正方形の面積
⊿(B,C)=B・C/2:直角三角形の面積
∴ x2+y2=z2
この定理は、フェルマーの最終定理に比べて人類の歴史に大きく貢献しているように思われます。
Cf)
x2+y2=z2
を満たす3数x、y、zを見つけ出すのは一見、難しそうに思えますが、そうでもありません。
x2=z2 -y2 =(z+y)・(z-y) を使うと、
x=3の場合、
32=9・1 より z+y=9、 z-y=1を解くことと同じなので、
32=((9+1)/2)2-((9-1)/2)2
=52 -42
有名な3、4、5の組み合わせが出てきます。連続する自然数でピタゴラスの定理を満たすのは、これだけです。
n2=(n+1)2 -(n-1)2 =4・n : n≠0
∴ n=4
これを一般化すると、
(2n+1)2=4n2+4n+1
=(2n(n+1)+1)2-(2n(n+1))2
(n+n+1)2+(2n(n+1))2=(2n(n+1)+1)2
手順
1) nとn+1を決めて、加算する。 2と3で、5
2) nとn+1を乗算して2倍する。 6の2倍で、12
3) 2)の結果に1を足す。 12足す1で、13
xが偶数の場合にはx=2・p・qとおいて、
x2=2p^2・2q^2=z2 -y2 =(z+y)・(z-y)
z+y=2p^2
z-y=2q^2
を解いて、 z=p^2+q^2 と y=p^2-q^2
2・p・q,p^2-q^2 ,p^2+q^2の組み合わせは、かなり昔から知られているものです。
・x2+y2=z2 : 直角三角形の3辺の関係
x・y=x+y+z=2(z+1) :面積の2倍が3辺の長さに等しい
これらの条件を満たす自然数x、y、zを求めよ。
x+y-z=2より x+y=z+2
(x+y)2 =(z+2)2
x2+y2+2x・y= z2 +4z+4
x・y=2(z+1)
x・y-2(x+y)=2(z+1)-2(z+2)=-2
x・y-2(x+y)+4=2
(x-2)(y-2)=2
よって 2=1・2=2・1より
x-2=1から x=3
y-2=2から y=4
または
x-2=2から x=4
y-2=1から y=3
x・y=2(z+1)=12から z=5
したがって、辺の長さ3、4,5の直角三角形が求まり、面積は6で、辺の和は12となる。
ヒトが3、4、5、6、12を見て直ちに気付くのは、偶然(!)にも1から6までの数字が全て現れていることである(ヒトは偶然を持て囃す生き物である)。
eの近似値
eは、自然対数の底などという堅苦しい名前で呼ばれていますが、
レオンハルト・オイラー(Euler)先生が使ったのでeになったのではないかと邪推しております。
アイザック・ニュートン氏は、1665年に
指数関数 exp(x)=Σx^k/k! :!は階乗
を示したそうです。
e=exp(1)=Σ 1/k!
を地道に計算すればいいのですが、短気な人には、
e=Σ((3k+2)^2+1)/(3k+2)!
がお勧めです。(さらに短気な人は? すでに退場していると思います。)
これは、ニュートンの式を3項ずつまとめたもので、
1/(k-1)!+1/k!+1/(k+1)!
=(1/k!)(k+1+1/(k+1))
=((k+1)^2+1)/(k+1)!
kを1つずらしてk-1にすれば
(k^2+1)/k!
となるので、憶えやすいです。
実際の計算を機械にやってもらうと、以下のようになりました。
k | 3k+2 | 3k+2 ! | (3k+2)^2+1 | 第k項 | 累積値 | 誤差 |
0 | 2 | 2 | 5 | 2.5 | 2.5000000000 | -0.21828 |
1 | 5 | 120 | 26 | 0.216667 | 2.7166666667 | -0.00162 |
2 | 8 | 40320 | 65 | 0.001612 | 2.7182787698 | -3.1E-06 |
3 | 11 | 39916800 | 122 | 3.06E-06 | 2.7182818262 | -2.3E-09 |
4 | 14 | 8.72E+10 | 197 | 2.26E-09 | 2.7182818285 | -8.2E-13 |
5 | 17 | 3.56E+14 | 290 | 8.15E-13 | 2.7182818285 | ほぼ0 |
k=2までの総和を分数で表すと、
e≒109601/40320
となって、簡単に記憶できます(ウソです)。
分子は109と601に分解して、601は109をひっくり返したものだから憶えやすい。
分母は4、3、2と減っていき、4と3の間と最後に0が入る・・・覚えにくーい。
実は、e=2.7 1828 1828 45 90 45・・・
なので、比較的記憶しやすいのでありました(それを最初に言えってか?)。
-
-
記憶バックアップ作戦
0











