記憶バックアップ作戦
ピタゴラスの定理
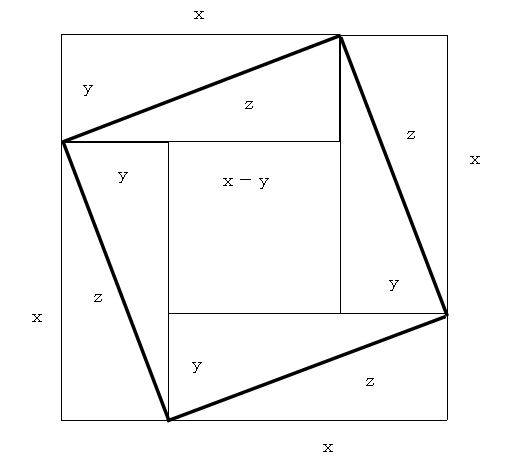
この図と同様のものが、今から二千年以上も前に、y:x:z=3:4:5の比率で描描かれていたことを知ったときには感心しました。ピタゴラスの定理は、彼が証明したときよりもさらに二千年以上前に発見されていたらしいとのことです。
ユークリッド先生が行った証明は私にはとても記憶できるような代物ではありません。以下の証明は、上図を記憶できるかどうかにかかっています。
大きい方の正方形から、
□(x+y)=4・⊿(x,y)+□(z)
小さい方の正方形から、
□(z)=4・⊿(x,y)+□(x-y)
が分かります。
□(A)=A・A :正方形の面積
⊿(B,C)=B・C/2:直角三角形の面積
∴ x2+y2=z2
この定理は、フェルマーの最終定理に比べて人類の歴史に大きく貢献しているように思われます。
Cf)
x2+y2=z2
を満たす3数x、y、zを見つけ出すのは一見、難しそうに思えますが、そうでもありません。
x2=z2 -y2 =(z+y)・(z-y) を使うと、
x=3の場合、
32=9・1 より z+y=9、 z-y=1を解くことと同じなので、
32=((9+1)/2)2-((9-1)/2)2
=52 -42
有名な3、4、5の組み合わせが出てきます。連続する自然数でピタゴラスの定理を満たすのは、これだけです。
n2=(n+1)2 -(n-1)2 =4・n : n≠0
∴ n=4
これを一般化すると、
(2n+1)2=4n2+4n+1
=(2n(n+1)+1)2-(2n(n+1))2
(n+n+1)2+(2n(n+1))2=(2n(n+1)+1)2
手順
1) nとn+1を決めて、加算する。 2と3で、5
2) nとn+1を乗算して2倍する。 6の2倍で、12
3) 2)の結果に1を足す。 12足す1で、13
xが偶数の場合にはx=2・p・qとおいて、
x2=2p^2・2q^2=z2 -y2 =(z+y)・(z-y)
z+y=2p^2
z-y=2q^2
を解いて、 z=p^2+q^2 と y=p^2-q^2
2・p・q,p^2-q^2 ,p^2+q^2の組み合わせは、かなり昔から知られているものです。
・x2+y2=z2 : 直角三角形の3辺の関係
x・y=x+y+z=2(z+1) :面積の2倍が3辺の長さに等しい
これらの条件を満たす自然数x、y、zを求めよ。
x+y-z=2より x+y=z+2
(x+y)2 =(z+2)2
x2+y2+2x・y= z2 +4z+4
x・y=2(z+1)
x・y-2(x+y)=2(z+1)-2(z+2)=-2
x・y-2(x+y)+4=2
(x-2)(y-2)=2
よって 2=1・2=2・1より
x-2=1から x=3
y-2=2から y=4
または
x-2=2から x=4
y-2=1から y=3
x・y=2(z+1)=12から z=5
したがって、辺の長さ3、4,5の直角三角形が求まり、面積は6で、辺の和は12となる。
ヒトが3、4、5、6、12を見て直ちに気付くのは、偶然(!)にも1から6までの数字が全て現れていることである(ヒトは偶然を持て囃す生き物である)。
eの近似値
eは、自然対数の底などという堅苦しい名前で呼ばれていますが、
レオンハルト・オイラー(Euler)先生が使ったのでeになったのではないかと邪推しております。
アイザック・ニュートン氏は、1665年に
指数関数 exp(x)=Σx^k/k! :!は階乗
を示したそうです。
e=exp(1)=Σ 1/k!
を地道に計算すればいいのですが、短気な人には、
e=Σ((3k+2)^2+1)/(3k+2)!
がお勧めです。(さらに短気な人は? すでに退場していると思います。)
これは、ニュートンの式を3項ずつまとめたもので、
1/(k-1)!+1/k!+1/(k+1)!
=(1/k!)(k+1+1/(k+1))
=((k+1)^2+1)/(k+1)!
kを1つずらしてk-1にすれば
(k^2+1)/k!
となるので、憶えやすいです。
実際の計算を機械にやってもらうと、以下のようになりました。
k | 3k+2 | 3k+2 ! | (3k+2)^2+1 | 第k項 | 累積値 | 誤差 |
0 | 2 | 2 | 5 | 2.5 | 2.5000000000 | -0.21828 |
1 | 5 | 120 | 26 | 0.216667 | 2.7166666667 | -0.00162 |
2 | 8 | 40320 | 65 | 0.001612 | 2.7182787698 | -3.1E-06 |
3 | 11 | 39916800 | 122 | 3.06E-06 | 2.7182818262 | -2.3E-09 |
4 | 14 | 8.72E+10 | 197 | 2.26E-09 | 2.7182818285 | -8.2E-13 |
5 | 17 | 3.56E+14 | 290 | 8.15E-13 | 2.7182818285 | ほぼ0 |
k=2までの総和を分数で表すと、
e≒109601/40320
となって、簡単に記憶できます(ウソです)。
分子は109と601に分解して、601は109をひっくり返したものだから憶えやすい。
分母は4、3、2と減っていき、4と3の間と最後に0が入る・・・覚えにくーい。
実は、e=2.7 1828 1828 45 90 45・・・
なので、比較的記憶しやすいのでありました(それを最初に言えってか?)。
円周率の近似値
π=N/M :NとMは互いに素な自然数
とおきます。
記憶障害を負った、どこかの博士が愛した数式
exp(iπ)+1=0 :iは虚数単位
を使うと、
exp(iN/M)= -1
exp(iN)=(-1)M
eとiとπと-1との間に何やら不思議な関係があるように見えますが、
eの指数の肩に乗せる数が実数である場合に周期性はなく、
eの指数の肩に純虚数を載せると周期性が生じて三角関数が現れます。
1のL乗根をexp(iX)と記すと、exp(iL・X)=1からL・X=2n・π
∴X=2π(n/L)
これは複素平面での単位円上に頂点をもつ正L角形を表しており、2π/Lをn倍する度に頂点が回転します。回転角度に関連するときにπが見えてきます。
余談ですが、オイラーの等式を、「おいらのとうしき」と発音した教授の言葉を真に受けて、その教授が発見した式だと思い込んでいた学生がいたらしい。
なお、オイラーの等式について、オイラー先生は何もコメントしていないので第1発見者ではなさそうです。円周率にギリシヤ文字πを使い始めたのはオイラー先生だと聞いています。
左辺はcos(N)+isin(N)
ゆえに
cos(N)=(-1)M
sin(N)=0
これを満たすNを探せばいいのですが、絶望的です(*1)。
とはいえ、sin(N)≒0を満たすNは何とか見つけられるはず。
あなたが計算の達人でなくとも、今の時代にはパソコンと表計算ソフトがありますから。
1から1000までの範囲でsin値を計算して、その絶対値を並べ替えると、
Ranking 1-1000 | N | abs(sin(N)) |
1 | 355 | 3.01444E-05 |
2 | 710 | 6.02887E-05 |
3 | 688 | 9.E-03 |
N=355を発見!
sinπ=0なので、 sin(355/M)≒0
より、同様の方法(*2)で、3<N/M<4の範囲でMを探索すると、
Ranking 88-118 | M | abs(sin(355/M)) |
1 | 113 | 2.66764E-07 |
2 | 114 | 0.027554078 |
3 | 112 | 0.028046525 |
M=113を発見!
結局
π≒355/113
これは3.141592920・・・で小数6桁まで合っています。
さて、記憶の仕方は、逆数の記号「\」を用いて、 :A\B=B/A
113\355
ですので、簡単カンタン。
しかし、人は簡単なものほど忘れる生き物ですから、そのときはアルベルトさん(*3)に頼りましょう。彼の誕生日は3月14日。悪しからず。
(*1)πは有理数でない(無理数)ので、自然数を用いた分数で表すことはできません。
π=3.14159265358979・・・と延々に続くので、愚鈍な小生は、記憶するのが無理な数を、無理数だと思っておりました。
(*2)この方法で次に見つかるのは、
103993/33102=3.141592653・・・ で小数9桁まで合っています。
312689/99532 (小数10桁)
833719/265381, 1146408/364913 (小数11桁)
5419351/1725033(小数13桁)
85563268/27235615 (小数15桁)
411557987/131002976 (小数16桁)
(*3)アルベルト・アインシュタイン
微分
-
-
記憶バックアップ作戦
0











